Hyperbolic Embedding에 관한 짧은 설명과 고찰- (1)

요즘 Non-Euclidean Embedding에 관한 논문들이 꽤나 나오고 있는데요?!

 

이게 수식도 어렵고 굳이 왜 이렇게 해야하나 싶더라구요.

(지난 게시글 chumji.tistory.com/2 에서 나온것처럼 torus에서의 euclidean distance가 적합하느냐 같은 질문도 들고....)

 

그래서 공부를 하다보니 Non-Euclidean Embedding에 대한 논문들을 알아보고 찾아보겠습니다.

그중 Hyperbolic Embedding에 대해서 여러 논문을 찾아보고 작성해보려고 합니다.

 

먼저 이를 Poincaré Embeddings for Learning Hierarchical Representations (Nickel. 2017)을 확인해 보겠습니다.

papers.nips.cc/paper/2017/file/59dfa2df42d9e3d41f5b02bfc32229dd-Paper.pdf

 

이는 Representation Learning을 쌍곡면 공간, 즉 Hyperbolic space에서 임베딩을 하고 이를 바탕으로 학습하는 방식으로 low-dimension에서 기존의 Euclidean 기반 Embedding기법에 비해서 좋은 성능을 보였습니다.

 

근데 Hyperbolic이 무엇이고 왜 여기다 임베딩을 해야 low-dim에서 좋고, 어떻게 연산을 해야하는지.....

이것들을 기록해주려 합니다!!! 해놓은 한글 블로그가 없어서 저도 슬펐어요

 

그렇다면 이제

1. Hyperbolic이 무엇이고, hyperbolic서 embed하는것은 무엇인가

2. 왜 이렇게 하는게 hyperbolic에서 embed하는게 low-dim서 좋은가

3. 어떻게 연산을 해야하는가

순으로 진행을 해볼게요

 

1. Hyperbolic이 무엇이고, hyperbolic서 embed하는것은 무엇인가?

출처 : Poincaré Embeddings for Learning Hierarchical Representations (Nickel. 2017)

출처 : Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry

 

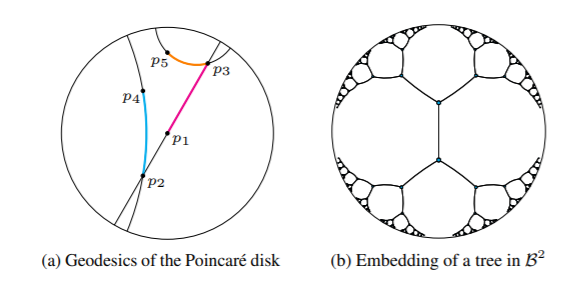
위 그림들 보이시죠? 저 맨 처음 원을 poincare disk, 이를 확장한 poincare ball이라 해요.

그리고 모든 쌍곡면 위의 점들을 이 원의 점들로 projection이 가능합니다.

이 쌍곡면 위의 점들로 embedding하고 이들을 원들의 점들로 대응하여 이해하는 것을 Hyperbolic Embedding이라고 합니다.

 

2. 왜 이렇게 하는게 hyperbolic에서 embed하는게 low-dim서 좋은가?

 

출처 : Curvature Regularization to Prevent Distortion in Graph Embedding

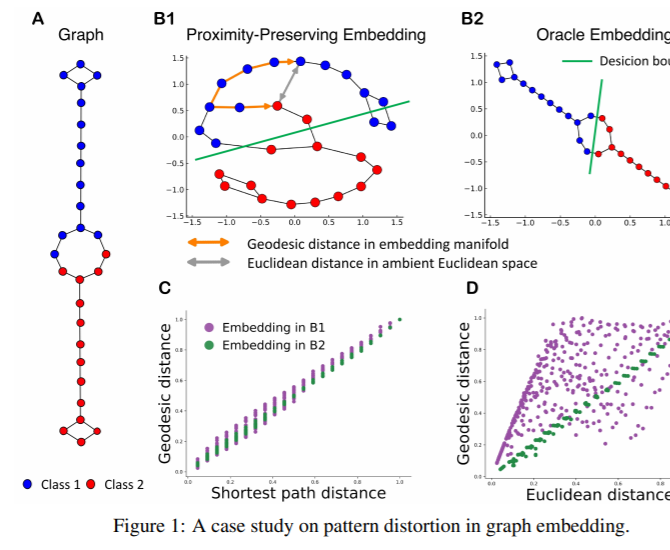
왜 Hyperbolic Embedding이 low-dim서 좋은 이유를 찾으면서 논문들을 찾았는데, 저는 NeurIPS 2020에 나온 Curvature Regularization to Prevent Distortion in Graph Embedding에서 제시한 이유가 적합하다고 생각했습니다.

 

이는 바로 hierarchical이나 relationship을 반영할때 기존의 학습방식처럼 proximity-preserving embedding을 euclidean space에서 하면 B1과 같이 embedding이 이루어져요.

이는 실제로는 엄청 멀어보이는 두 노드들 (예를 들면 B1왼쪽 아래 빨강과 초록색 선 위의 파랑) similar하게 판별하게 되는 문제가 생깁니다.

그리고 D에서와 같이 임베딩간의 euclidean distance가 실제 구조적 거리를 잘 반영하지 못하는 문제가 생기죠.

(제가 보기엔 맞는 것 같은데 어떠신가요?!)

 

하지만 이를 옆에 oracle embedding(B2)의 모양처럼 학습하게하는 방법들이 있으면 좋겠지만, 구조가 복잡해지고 각 object들의 feature정보도 들어간다면 그렇게 하기가 더욱 힘들어질거에요ㅠㅠㅠㅠㅠㅠㅠㅠ

하지만 일종의 제약(쌍곡면공간)을 주어 proximity-preserving하게 하는 모델들이 oracle embedding에 가깝게 갈수있을겁니다.

 

 

3. 어떻게 연산을 해야하는가?

 

이번 포스트 Hyperbolic Embedding에 관한 짧은 설명과 고찰 - (1)에서는 왜 기존 연산과 다른 연산이 hyperbolic embedding에서 필요한지까지만 알아보고 이후는 다음에 알아보도록 할게요;;; (분량이 길어져....)

출처 : Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry

 

아까 잠시 언급한 것 처럼 hyperbolic embedding하기 위해서는 poincare ball과 이 ball에 대응하는 projection값이 필요하다고 했죠?

아래처럼 수식처럼 Poincare Ball인 D^n안의 실수 공간에서 있는 x를 

Hyperboloid공간과 Poincare Circle을 대응하는 법

 

그리고 이 대응하는 원위의 점들은 기본적으로 hyperboloid공간의 점을 표현하는 방법이므로, 이 hyperboloid공간에 맞는 연산을 통해 distance를 구하고, matrix multiply를 하고 back-prop을 하는 과정이 필요합니다.

이를 위해 여러 논문들에서 이러한 연산들을 제안합니다.

 

 

 

그럼 다음 포스트에서 연산방법을 알아보도록 할게요 안뇽~~~