고정 헤더 영역
상세 컨텐츠
본문
안녕하세요!!!! 다시 돌아온 초보대학원생입니다.
오늘은 어제 포스팅 chumji.tistory.com/3의 다음 파트인 hyperbolic embedding의 연산에 대해 알아보겠습니다.
3. Hyperbolic embedding의 연산 방법
Hyperbolic embedding의 연산이 기존의 우리가 아는 연산과 다른 이유는, hyperbolic space위의 점들을 poincare disk위로 projection하는 과정에서 생긴다고 확인했는데요.
이제 그 disk위에서의 각 점을 식으로 표현해보겠습니다.
이를 위해서 우리는 manifold를 사용한다고 하네요.....
으앙 이건 뭐지? 하는 분들을 위해 좀더 자세하게 설명해보겠습니다.
일단 식을 보죠!
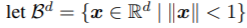
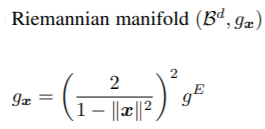
무슨 말인지 잘 모르시겠죠? 저도 그랬어요.
공간을 정의하기 위해서는, 크게 그 공간의 정의되는 공간과 metric (=공간의 점을 측정하는 방법)이 필요로 한다하네요!!!
일반적으로 우리가 아는 피타고라스 정리를 이용한 것이 일반적인 Euclidean 공간에서의 metric입니다.
마치 2차원 공간에서 (u,v)에 대한 metric은 u^2 + v^2입니다! (쉽죠?)
이에 앞에 다음과 같이 곱해준 것이 hyperbolic 공간에서의 metric입니다.
똑같이 (u,v)에 대해서 다음과 같이 나타내진다고 하네요.

오 이제 좀 이해가 되는 것 같지 않으신가요?
제가 이용한 링크를 www.ru.ac.za/media/rhodesuniversity/content/mathematics/images/ggc/Talk-2010-09-Henninger-RU-Hyp.pdf 첨부할게요! 더 자세한 이해를 위해서 확인해보셔도 좋을 듯 합니다.
하 무엇을 위해 이 고난길을 간단 말인가 추욱 쳐지네요ㅠㅠㅠㅠ
하지만 이제 거의 왔습니다 쫌만 버텨보아요.
먼저 각 점에서의 metric을 알아보았으니, 이제 무엇이 필요할까요?
맞아요! 두 점 사이의 거리겠죠?
수학은 참 어려운데 수긍되는 말만해서 얄미운 존재.....
이제 distance를 정의해볼게요!
이는 아까 우리가 본 metric에서 곱한 것을 똑같이 distance에 곱해주고 이를 좀만 바꿔주면 됩니다.

이렇게 우리가 아는 distance에서, 각 점의 metric서 곱해준 것 처럼 1-norm의 역수를 곱해주겠죠?
여기까진 자연스러운데 transform을 하고, arcosh를 취해주네요.

이렇게 거리를 깔끔하게(?) 정의했다면, 막상 objective function 자체는 단순합니다.
물론 차후 논문들은 이를 점점 확장시켰지만요!!!

짠!!! 머리가 지끈지끈하시죠?ㅠㅠㅠㅠ
그럼 저도 더욱 공부해서 저 arcosh를 해결하고 와야겠네요.
이상으로 간단하게 hyperbolic embedding을 사용하는 이유와, 공간 정의법, 이를 활용한 학습법에 대해서 굉장히 naive하게 알아보았습니다.
이는 무긍무진하게 활용되니 같이 공부해보면 좋을 것 같아요!
'딥러닝 논문리뷰' 카테고리의 다른 글
| CS330 들으며 Meta-Learning 정리해보기 - (1) (0) | 2020.12.31 |
|---|---|
| Attention과 Norm의 관계 (1) | 2020.12.29 |
| Hyperbolic Embedding에 관한 짧은 설명과 고찰- (1) (2) | 2020.12.26 |
| TorusE : 리 군을 활용한 지식 그래프 임베딩 (1) | 2020.12.16 |





댓글 영역